
Ideas of Bernhard Riemann in his 1859 paper on the zeta-function sketched an outline for proving the conjecture of Legendre and Gauss. A weaker consequence of this high density of primes was Bertrand's postulate, that for every n > 1 n>1 there is a prime between n n and 2 n 2n, proved in 1852 by Pafnuty Chebyshev. A simple but slow method of checking the primality of a given number n n, called trial division, tests whether n n is a multiple of any integer between 2 and n, where log x \log x is the natural logarithm of x x. The property of being prime is called primality. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself.
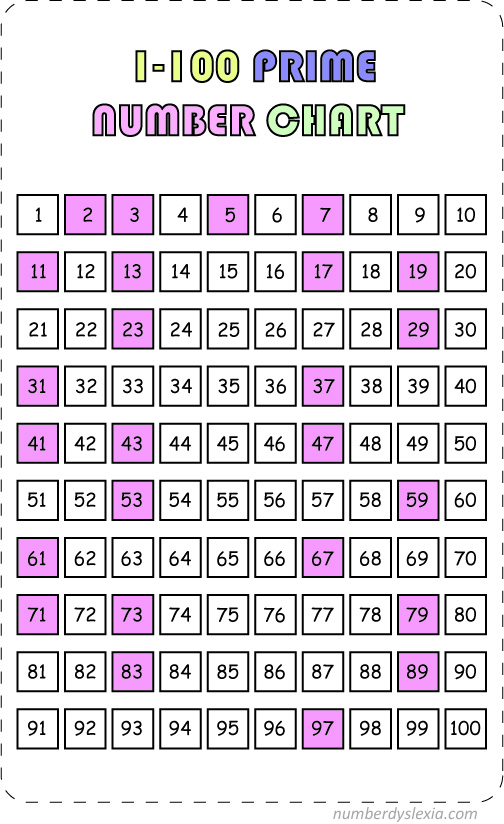
A natural number greater than 1 that is not prime is called a composite number.


For other uses, see Prime (disambiguation).Ĭomposite numbers can be arranged into rectangles but prime numbers cannot.Ī prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers.


 0 kommentar(er)
0 kommentar(er)
